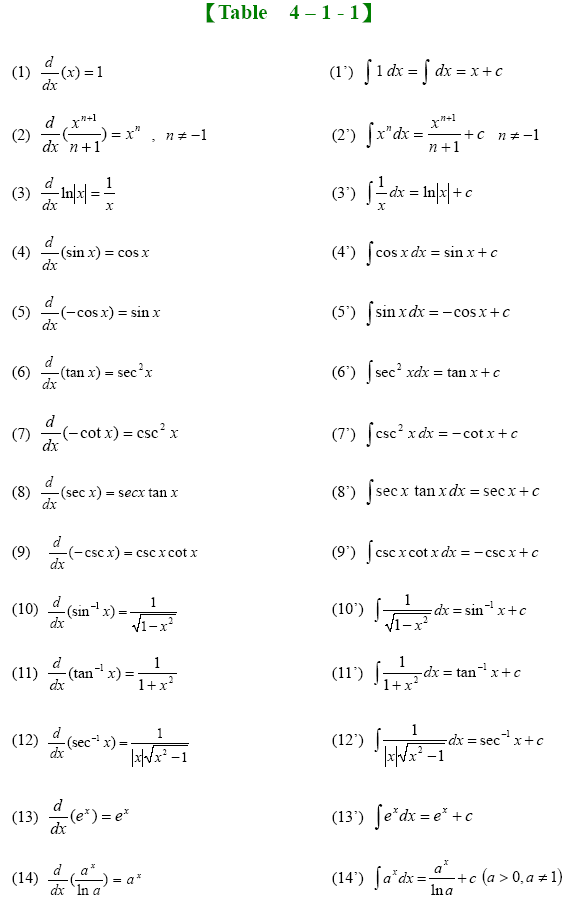()0 d c dx =, c is any constant. Must know derivative and integral rules! Downloaded from sae international by a s emam, thursday, march 29, 2018 2 optimized proportional integral derivative controller of vehicle active suspension system the performance of active systems during the last three table 1 quarter vehicle suspension parameters [19].
Excel in Kinematics
If c ts a constant then:
U0 = du dx is the derivative of u with respect to (w.r.
Calculus trigonometric derivatives and integrals trigonometric derivatives d dx (sin( x)) = cos( )·0 d dx (cos( )) = sin(0 d dx (tan( x)) = sec2( )· 0 d dx (csc( x)) = csc( )cot( )·0 d dx (sec( )) = sec( )tan(0 d dx (cot(x)) = csc2( x)· 0 d dx (sin 01 (x)) =p 1 1x2 ·xd dx (cos (tan1(x)) = p 1 1x2 0 d dx 1 1 1+x2 ·x 0 d dx (csc 1(x)) = 1 x p x21 ·x0 d dx (sec (cot1 (x)) =1 x p x21 ·x0 d. Dx du v dx dv (uv) u dx d = + 4. Table of integrals basic forms (1)!xndx= 1 n+1 xn+1 (2) 1 x!dx=lnx (3)!udv=uv!vdu (4) u(x)v!(x)dx=u(x)v(x)#v(x)u!(x)dx rational functions (5) 1 ax+b!dx= 1 a ln(ax+b) (6) 1 (x+a)2!dx= 1 x+a (7)!(x+a)ndx=(x+a)n a 1+n + x 1+n #$ % &', n!1 (8)!x(x+a)ndx= (x+a)1+n(nx+xa) (n+2)(n+1) (9) dx!1+x2 =tan1x (10) dx!a2+x2 = 1 a tan1(x/a) (11) xdx!a2+x2. Generally, if the function is any trigonometric function, and is its derivative, ∫ a cos n x d x = a n sin n x + c {\displaystyle \int a\cos nx\,dx={\frac {a}{n}}\sin nx+c} in all formulas the constant a is assumed to be nonzero, and c denotes the constant of integration.
Constant rule, [ ]c =0 dx d 6.
Quotient rule v2 vu uv v u dx d ′− ′ = 5. If a term in your choice for yp happens to be a solution of the homogeneous ode corresponding to (4), multiply this term by x (or by x 2 if this solution corresponds to a double root of the Derivative and integral table (and other pages of use) c18. Integration is the basic operation in integral calculus.
Power rule [ ]x =1 dx d 8.
The table below is intended to assist people working with the alternative calculus called the geometric calculus (or its discrete analog). Derivatives derivative applications limits integrals integral applications integral approximation series ode multivariable calculus laplace transform taylor/maclaurin series fourier series. C, n, and a > 0 are constants; V2 dx dv u dx du v v u dx d − = 6.
Table of integrals ∗ basic forms z xndx = 1 n +1 xn+1 (1) z 1 x dx =ln|x| (2) z udv = uv z vdu (3) z 1 ax + b dx = 1 a ln|ax + b| (4) integrals of rational functions z 1 (x + a)2 dx = 1 x + a (5) z (x +.
It is a pdf file document. Constant multiple rule [ ]cu cu dx d = ′, where c is a constant. Calendar inbox history help close. Common derivatives and integrals derivative rules:
_f(e1) (xl a) second rectangle area is:
Line equations functions arithmetic & comp. Sum and difference rule [ ]u v u v dx d ± = ±′ 3. Derivative involving absolute value [ ]= ( )u′,u ≠0 u u u. Differentiation formulas d dx k = 0 (1) d dx [f(x)±g(x)] = f0(x)±g0(x) (2) d dx [k ·f(x)] = k ·f0(x) (3) d dx [f(x)g(x)] = f(x)g0(x)+g(x)f0(x) (4) d dx f(x) g(x.
While differentiation has straightforward rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful.
Derivative and integral table (and other pages of use) skip to content. Table of integrals∗ basic forms z xndx = 1 n+ 1 xn+1 (1) z 1 x dx= lnjxj (2) z udv= uv z vdu (3) z 1 ax+ b dx= 1 a lnjax+ bj (4) integrals of rational functions z 1 (x+ a)2 dx= ln(1 x+ a (5) z (x+. Dx du (cu) c dx d = 3. _f(e2) (x2 xl) if axk — x k x then the area ts:
This page lists some of the most common antiderivatives.
To) x (1) x0 = 1 (2) c0 = 0 (3) (cu)0 = c·u0 (4) (u±v) 0= u0 ±v (5) (uv) 0= u v +v0u (6) u v 0 = u0v −v0u v2 (7) (un) 0= nun−1u (a) 1 u 0 = − u0 u2 (b) (√ u)0 = u0 2 √ u Integrattm ranges can be changed according to the rule: The integral can be calculated by ftnddtng the sum of each rectangle area: Dx dv dx du (u v) dx d ± = ± 2.
Area = lim axk = f (x)dx and g — g(x) then:
Power rule [ ] u nu u dx d =n −1 ′ 7. A very complete table of common formulas for derivatives and integrals as well as procedures. Product rule [ ]uv uv vu dx d = +′ 4. Dx dv wu dx du vw dx dw (uvw) uv dx d = + + 5.
(chain rule) if y = f(u) is differentiable on u = g(x) and u = g(x) is differentiable on point x, then the composite function y = f(g(x)) is differentiable and dx du du dy dx dy = 7.
Table 2.1, choose yp in the same line and determine its undetermined coefficients by substituting yp and its derivatives into (4). © 2005 paul dawkins integrals basic properties/formulas/rules òòcf(x)dx= cf(x)dx, c is a constant. U = u(x) and v = v(x) are differentiable functions of x; Interested readers are encouraged to improve the table by inserting citations for verification, and by inserting more functions and more calculi.
General rules derivative rule integration rule sum/di erence rule sum/di erence rule d dx f (x)g =0 r dx r r constant multiple rule constant multiple rule d dx cf (x) =0 r dxc r f product rule integration by parts d dx f (x)g = 0) + r dx r quotient rule (no simple rule corresponds) d dx h f (x) g(x) i = 0 g0 [g(x)]2