Conservation of momentum is represented in the traditional vectorial fashion at top and the more novel total area of mass versus velocity before and after the collision below. The final velocity of a system in an inelastic collision is : From conservation of momentum for totally inelastic collisions:
Explaining ideal gas behavior
Fill in the start conditions:
V f = m 1v 1i + m 2v 2i m
2i only requires the following conservation of momentum equation to determine the final velocity v f of the two objects. We know that the formula for momentum is given as formula: That is, the total initial momentum of the system p~i is equal to the total final momentum p~f: The final velocity of the second piece after an explosion is :
Then fill in either the mass of b or the final velocity of a+b.
I) total momentum before collision when both objects move in same direction using the law of conservation of momentum, p before collision = m 1 u 1 + m 2 u 2. Total momentum before collision when both objects move in the same direction is 575kg.m/s An inelastic collisions occurs when two objects collide and do not bounce away from each other.momentum is conserved, because the total momentum of both objects before and after the collision is the same. Elastic and inelastic collisions equations.
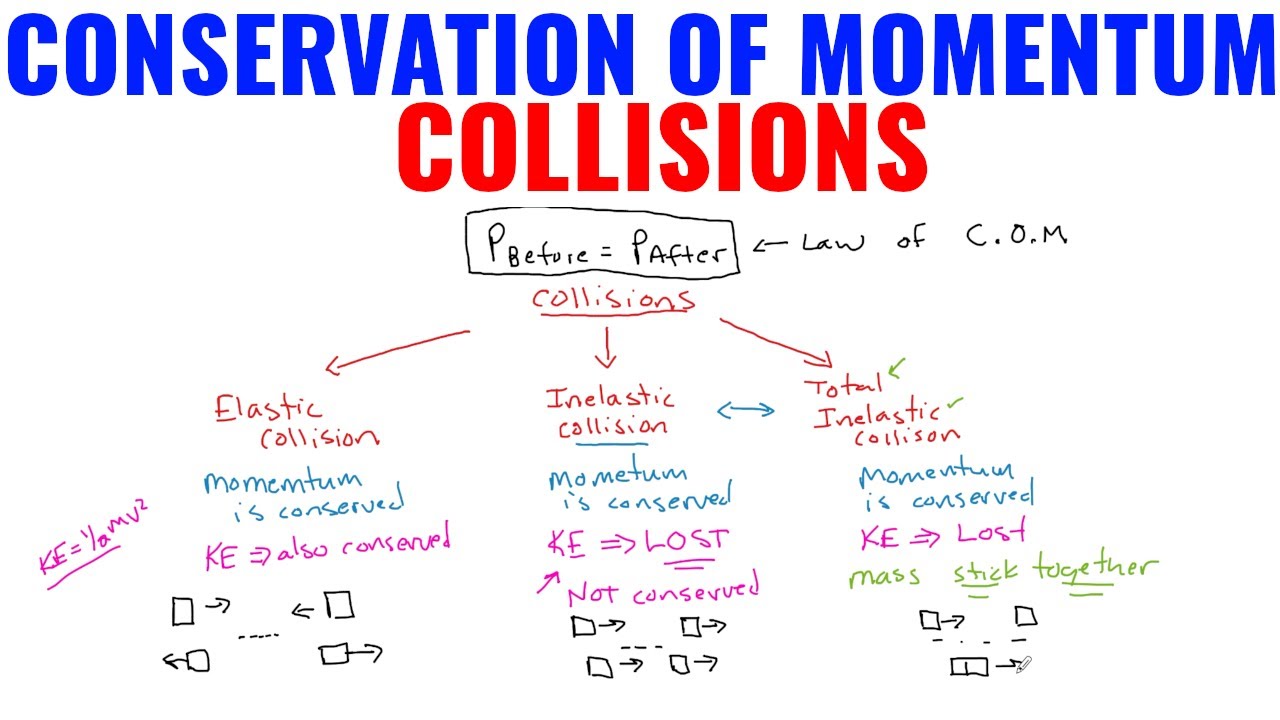
An inelastic collision is any collision between objects in which some energy is lost due to it.
The final momentum of the first object is equal to 8 kg * 4 m/s = 32 n·s. A special case of this is sometimes called the perfectly inelastic collision. In this topic, we will discuss. Calculate the momentum of the system before the collision.
Complete applet with all features shown for the case of an elastic collision.
Substituting all values, p before collision = 15 x 25 + 10 x 20. Conservation of momentum collision before and after stock illustration. From, law of conservation of momentum we get to know that, p initial = p final M 1 v 1i + m 2 v 2i = (m 1 + m 2) v f it can be shown that in totally inelastic collisions, the kinetic energy of the
In a perfectly inelastic collision, two objects collide and stick together.
Physically the two objects each have different initial velocities and “stick” together with one final velocity: Kinetic energy is not conserved, but the result is easy to calculate via conservation of momentum. Mass and velocity of a. In totally inelastic collisions, both objects stick to each other after the collision, therefore there is only one final velocity to find, v 1 f = v 2 f = v f.
The law of conservation of momentum states that all momentum is conserved in a collision.
According to the law of conservation of momentum, total momentum must be conserved. An elastic collision occurs when both the kinetic energy (ke) and momentum (p) are conserved. The calc will provide the unknown mass or velociy of b. Consequently, is momentum conserved in elastic and inelastic collisions?
Conservation of momentum in an inelastic collision.
P~ t ˘m1 ~v1 ¯m2v~2 ¯¢¢¢¯mnv~n (2.2) when the sum of external forces acting on a system is zero, momentum is conserved. Mass of body 2 = m 2 the initial velocity of body 1 = u 1 the initial velocity of body 2 = u 2 P before collision = 575. Two pool balls colliding on a pool table is an example.
Inelastic collision equation (objects combine and stick together) m 1 v 1i + m 2 v 2i = v f (m 1 + m 2)
Conservation of momentum is conserved and kinetic energy is conserved and no heat given off. Completely inelastic collisions involve objects which stick together afterwards. In any closed system, momentum is conserved. Final velocity of the second object in an elastic collision calculation;
Momentum is defined as p = mv.
And all the collisions were elastic in nature i.e. This collision is guided by the laws of motions and momentum conservation laws. Conservation of linear momentum is based on newton’s second law of motion which states that in an isolated system the total momentum remains the same. Let’s consider the following example, remember:
For momentum, you measure the masses of the objects and test to what degree the velocities support the law of conservation of momentum.
The total momentum p~t of a system of n discrete parts can be expressed as the sum of each of the parts: Momentum but not kinetic energy is conserved within the system; Thus, it is possible to equate momentum in the start and final states of a system and thus calculate an unknown. A special case of this is also called the perfectly inelastic collision.
In the above experiment we did not consider any loss of energy due to friction , heat, etc.
In such a collision in which kinetic energy of the system is not conserved but the momentum is conserved. In an elastic collision, both momentum and kinetic energy are conserved. When a collision occurs, most of the time a lot of. The inelastic collision formula is articulated as.
In this case, initial momentum is equal to 8 kg * 10 m/s + 4 kg * 0 m/s = 80 n·s.
The crash in which kinetic energy of the system is not conserved but the momentum is conserved, then that collision is termed as inelastic collision. F = mv f = p i = m 1v 1i + m 2v 2i equation 1 is the solution of the final velocity for an inelastic collision. The momentum of the objects before the collision is conserved, but the total energy is not conserved. An inelastic collision is any collision between objects in which some energy is lost.
Where mass of body 1 = m 1.
Partially inelastic collisions involve objects which separate after they collide, but which are deformed in some way by the interaction.