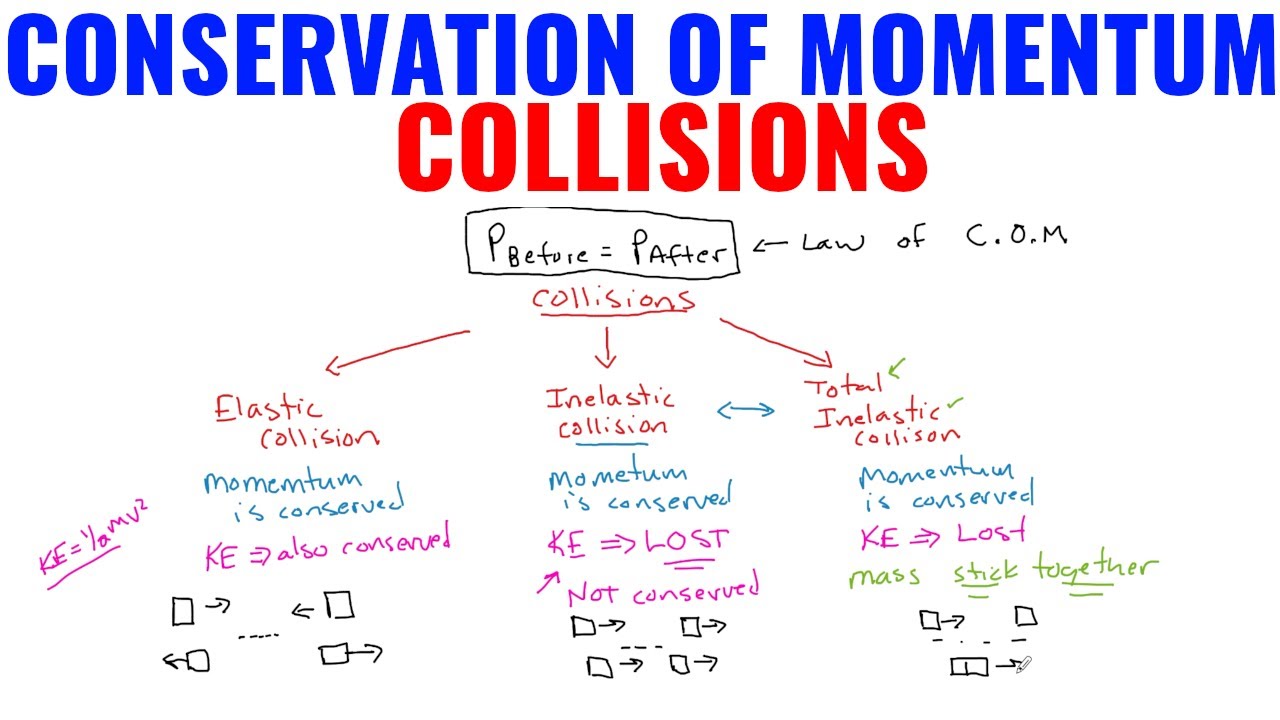
From, law of conservation of momentum we get to know that, p initial = p final After colliding the two objects bounce off each other. Inelastic collision equation (objects combine and stick together) m 1 v 1i + m 2 v 2i = v f (m 1 + m 2)
PPT Impulse Momentum The impulsemomentum theorem
As momentum is a vector equation and there is one conservation of momentum equation.
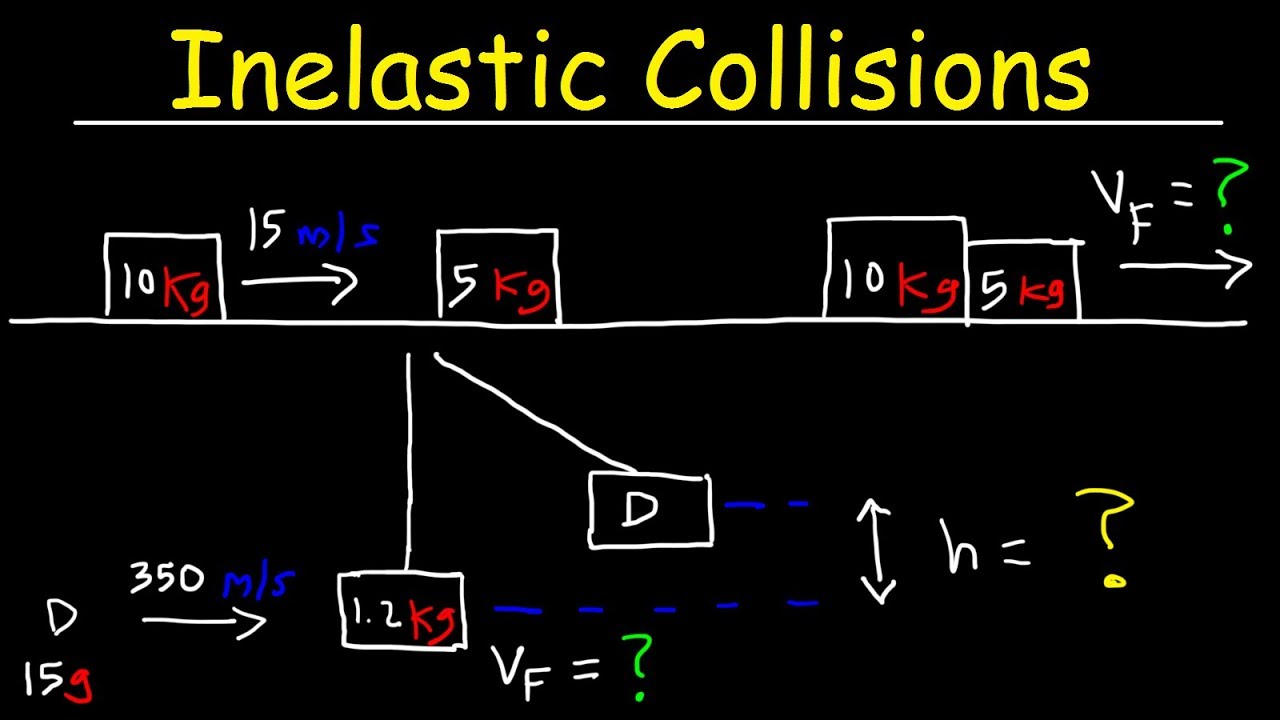
This physics video tutorial explains how to solve inelastic collision problems in one dimension using the law of conservation of linear momentum.
The total momentum p~t of a system of n discrete parts can be expressed as the sum of each of the parts: So the total momentum before an inelastic collisions is the same as after the collision. P~ t ˘m1 ~v1 ¯m2v~2 ¯¢¢¢¯mnv~n (2.2) when the sum of external forces acting on a system is zero, momentum is conserved. Kinetic energy is conserved in elastic collisions.
M 1 u 1 = (m 1 + m 2)v.
1 ’ • 96 + 60 = 37v. The final momentum of the first object is equal to 8 kg * 4 m/s = 32 n·s. Conservation of momentum is represented in the traditional vectorial fashion at top and the more novel total area of mass versus velocity before and after the collision below. Complete applet with all features shown for the case of an elastic collision.
Know the difference between elastic and inelastic collisions collisions between objects transfer momentum from one object to another.
The kinetic energy is transformed from or into other kinds of energy. Similarly, there will be only one conservation of energy equation. 2 = 12 m/s east. The crash in which kinetic energy of the system is not conserved but the momentum is conserved, then that collision is termed as inelastic collision.
After colliding the two objects.
In an inelastic collision kinetic energy is not conserved, but momentum is conserved. When a shot is fired from a gun, the gun recoils. For example, a fast moving trolley runs into a brick wall, after hitting. Size 12{m rsub { size 8{1} } v rsub { size 8{1} } = left (m rsub { size 8{1} } +m rsub { size 8{2} } right )v'} {}
Momentum but not kinetic energy is conserved within the system;
For momentum, you measure the masses of the objects and test to what degree the velocities support the law of conservation of momentum. Unit 3:collisions and conservation of momentum essential concept 3d: After an inelastic collision the two objects are stuck together, and thus travel with the same final velocity; Momentum is defined as p = mv.
When the shot is fired, it leaves the barrel with a certain force.
One must use both conservation of energy and conservation of momentum to figure out the motions of the objects afterwards. • anything at rest before? The law of conservation of momentum states that all momentum is conserved in a collision. Where mass of body 1 = m 1.
In the special case where two objects stick together when they collide, the fraction of the kinetic energy which is lost in the collision is determined by the combination of conservation of energy and conservation of momentum.
According to the law of conservation of momentum, total momentum must be conserved. Mass of body 2 = m 2 the initial velocity of body 1 = u 1 the initial velocity of body 2 = u 2 That is, the total initial momentum of the system p~i is equal to the total final momentum p~f: Momentum is conserved in inelastic collisions, but one cannot track the.
Any macroscopic collision between objects will convert some of the kinetic energy into internal energy and other forms of energy, so no large scale impacts are perfectly elastic.
Viewgraph 1 viewgraph 2 viewgraph 3 viewgraph 4 viewgraph 5. In this case, initial momentum is equal to 8 kg * 10 m/s + 4 kg * 0 m/s = 80 n·s. 1 ’ = 37 kg. One of the practical results of this expression is that a large object striking a very small object at rest will lose very.
M 2 = 5 kg.
Thus, the conservation of momentum equation simplifies to m 1 v 1 = m 1 + m 2 v ′. When a collision occurs, most of the time a lot of velocity is lost and most of the mass remains. M 1 v 1 = m 1 + m 2 v ′. An inelastic collision is a collision in which total momentum is conserved but total kinetic energy is not conserved.
Visit stack exchange tour start here for quick overview the site help center.
• list given information • write correct equation • substitute • solve • collision • inelastic • no • m. Conservation of momentum in an inelastic collision. 1 = 32 kg v 1 = 3 m/s east. V = (m1v1+m2v2)(m1+m2) where, v= final velocity of the object.
When two objects collide with each other under inelastic conditions, the final velocity of the object can be obtained as;
Calculate the momentum of the system before the collision. M1 u1 +m2 u2 ’=’m1 v1 +m2 v2 example: E f = ½ (m 1 + m 2)v 2, e i = ½ m 1 u 1 2. An inelastic collision is one in which part of the kinetic energy is changed to some other form of energy in the collision.
We know that the formula for momentum is given as formula:
This fact, together with conservation of momentum, allows the final motion of the two. M1= mass of the first object (kg) m2= mass of the second object (kg) v1 = initial velocity of the first object (m/s) Total momentum before collision ‘=’ total momentum after the collision. 1 ’ • 32(3) + 5(12) = 37v.
According to the law of conservation of momentum, for a collision between two bodies.
The inelastic collision formula is articulated as.