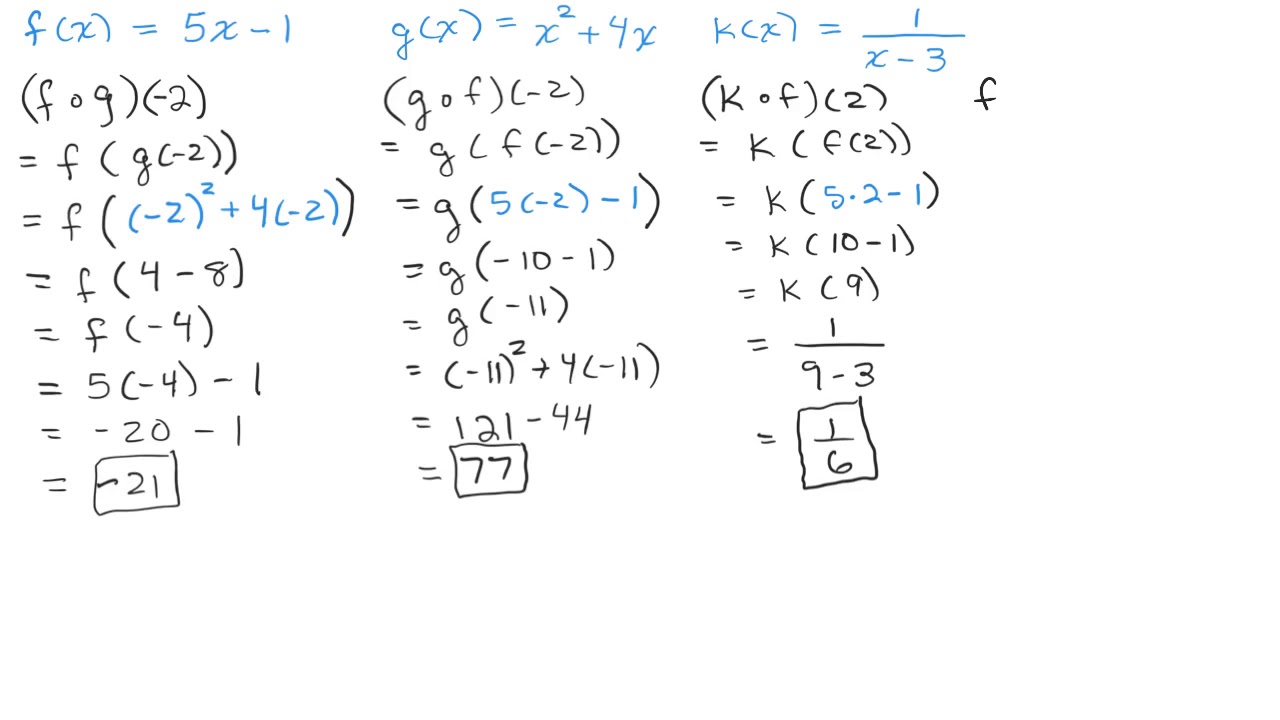The composite function’s domain will be the resultant set of both domains. Composition of a function is done by substituting one function into another function. Suppose f is a function, then the composition of function f with itself will be (f∘f)(x) = f(f(x)) let us understand this with an example:
Composition of Functions YouTube
Discover more science & math facts & informations.
The values coming out of a function are.
These functions can be very useful when we have to model different processes with different functions. The order of composition is important when dealing with composition of functions examples. The mother function $m$ is a function that takes a person $x$ as an input and output that person's mother $m(x)$. Let us try to solve some questions based on composite functions.
If {eq}h(x) = 3x {/eq} and {eq}k(x) =.
G(f (x)) g ( f ( x)) evaluate g(3x+ 5) g ( 3 x + 5) by substituting in the value of f f into g g. Let's look at another composite function example. For example, f(g(x)) is the composite function that is formed when g(x) is substituted for x in f(x). We can form the grandmother $g$ function by composing the mother function with itself.
Here, we will explore a brief overview of function composition and we will.
( f ∘ g) ( x) w h e r e f ( x) = 5 x − 1 a n d g ( x) = 4 3 x − 2. Answers to composite functions examples (id: Now, x normally has the domain of all real numbers. A composition of functions is formed by taking the outputs of one function and converting them into the inputs of another function.
5 rows composite functions are operations that take two or more functions as one function such as.
Here are some examples of finding the domain of composite functions. The composite function f [g (x)] is read as “f of g of x”. For the composition of a function, we take (o). Some examples example (f o g) (x) = f [g (x)] (g o f) (x) = g.
Example 1 if {eq}f(x)\ =\ 3\cdot x {/eq} and {eq}g(x)\ =\ x\ +\ 5 {/eq}, what is the domain of g(f(x)) ?
G was the function performed on x. For example, f[g(x)] is the composite function of f(x) and g(x). Example of composition of functions Here, we demonstrate the process of composing functions with a series of examples.
F (x) = x + 1 f ( x) = x + 1 , g(x) = x2 g ( x) = x 2 , g(f (x)) g ( f ( x)) set up the composite result function.
2 find the output for the inner function and substitute it into the expression for the outer function. A composite function is created when one function is substituted into another function. If f(x) = 3x 2, then find (f∘f)(x). Learn more about composition of functions here.
The steps of solving a composite function are as follows:
G(3x+5) = (3x+5)3 g ( 3 x + 5) = ( 3 x + 5) 3. G(f (x)) g ( f ( x)) evaluate g(x+ 1) g ( x + 1) by substituting in the value of f f into g g. F (x) = 3x + 5 f ( x) = 3 x + 5 , g(x) = x3 g ( x) = x 3 , (g ∘ f) ( g ∘ f) set up the composite result function. (g º f) (x) = g (f (x)) = (√x)2.
Given the function f(x) = 3x + 5 and g (x) = 2x3 2 x 3.find ( gof) (x) and ( fog) (x).
Finding the domain of a composite function. F(g(x)) is read as “f of g of x”. Finding the composition of two functions is what solving a composite function implies. F (x) = √x and g (x) = x2.
The following diagram shows some examples of.
F(g(x)) can also be written as (f ∘ g)(x) or fg(x), in the composition (f ∘ g)(x), the domain of f becomes g(x). The domain of g (x) = x2 is all the real numbers. G(x+1) = (x+1)2 g ( x + 1) = ( x + 1) 2. For example, the functions given by and can be combined to form the sum, difference, product, and quotient of and.
Here are some composition of function examples that you can use to better understand this mathematical operation.
A composite function is generally a function that is written inside another function. The above function can be broken down as a. F(x) = 3x 2 (f∘f)(x) = f(f(x)) = f (3x 2) = 3(3x) 2 = 3.9x 2 = 27x 2. Use the number to be evaluated as the input for the inner function and substitute it into the expression.