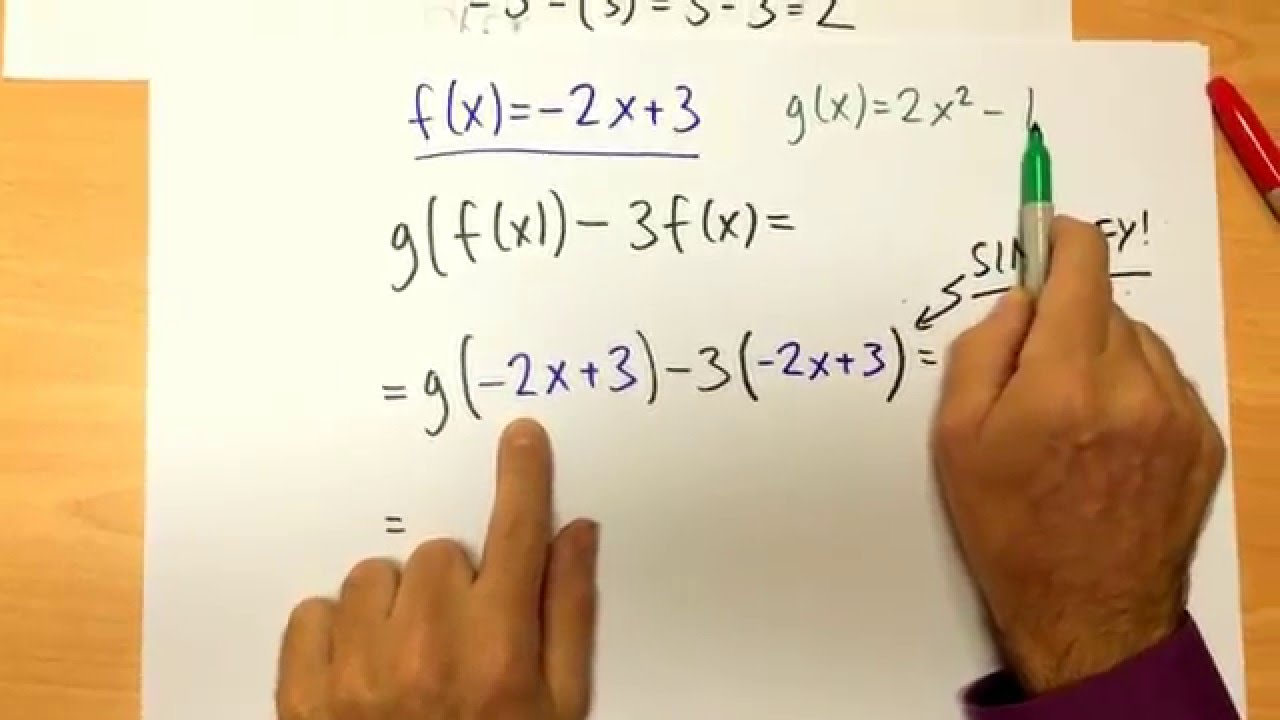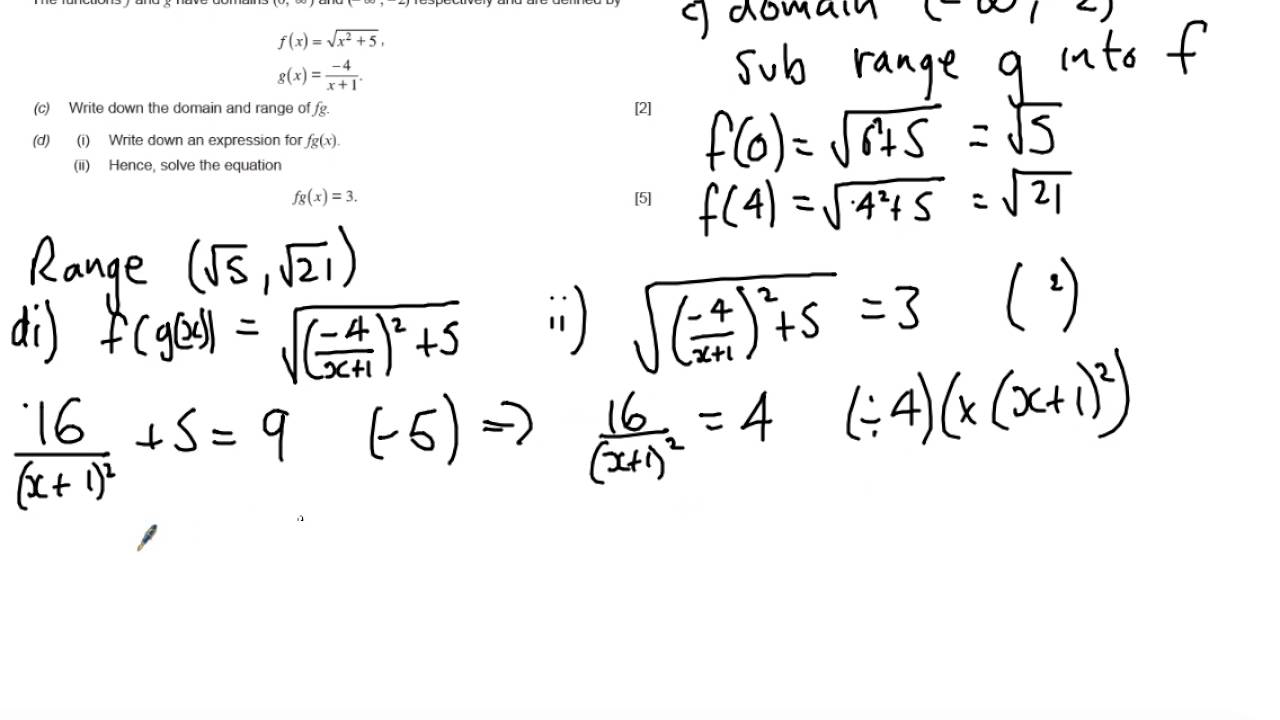If playback doesn't begin shortly, try. Gf is called the composite function of f and g. If f(x) = 3x 2, then find (f∘f)(x).
Composite Functions, Example 3 Using Graphs to Solve for
Examples, solutions, worksheets, games and activities to help precalculus students learn about composite functions.
For example, if t (y) is the temperature in the atmosphere as a function of height, and h (t) is the height of a weather balloon as a function of time, then t (h (t)) is the temperature at.
A) (f ∘ g) ( x) b) (g ∘ f) ( x) What is a composite function? In the composition (f ∘ g) ( x ), the domain of f becomes g ( x ). This instructional aid was prepared by the tallahassee community college learning commons.
If f and g are defined by f (x) = and g (x) = 5x + 3 , find (f o g) (x) = f (g (x)) sol’n:
Finding composite functions by plugging in another function. Try the free mathway calculator and problem solver below to practice various math topics. An example of a composite function. How to answer questions on composite functions?
For example, the functions given by and.
This function maps x directly to the function value g(f(x)). Composition of functions given by their formulas functions \( f \) and \( g \) are defined by the formulas: Try the free mathway calculator and problem solver below to practice various math topics. = f (g (x)) = f (5x + 3) =.
Let us try to solve some questions based on composite functions.
From the above equation, we can deduce that, u(x) = x3 v(x) = x−1 x u ( x) = x 3 v ( x) = x − 1 x. F(x) = 3x 2 (f∘f)(x) = f(f(x)) = f (3x 2) = 3(3x) 2 = 3.9x 2 = 27x 2. The following diagram shows some examples of composite functions. 84chapter 1 functions and their graphs.
Scroll down the page for more examples and solutions.
Example of composition of functions In other words, the long arrow produces the same result as the end result of the 2 short arrows in 2 “hops”. So it is onto function. Try the given examples, or type in your own.
Composite functions examples with solutions solve and simplify the given problems.
The composition (f o g) (x) of f(x) = x + 1 , g(x) = 3x is given by (f o g) (x) = f(g(x)) = g(x) + 1 = 3x + 1 since the domain of both functions is the set of all real numbers, the composition (f o g) (x) also have the set of all real numbers as its domain. The composite function is undefined for x ∈] a; For all y ∊ b, there is a preimage in a. B) find the composite function \( (f_o g)( x ) \).
F(x) = 3x − 5.
The above function can be broken down as a composition of two separate functions, f(x) =u(v(x)) =( x−1 x)3 f ( x) = u ( v ( x)) = ( x − 1 x) 3. The functions f,g, and h are defined for x ∈ ℝ, by f(x) = 2x + 1, g(x) = x 2, h(x) = 1/x. For all x ∊ a, we get different values of y ∊ b, so it is one to one function. Solutions to the above questions.
A composite function is a combination of function where the output of one function becomes the input of the next function.
Hence it is bijective function. F(x) =( x−1 x)3 f ( x) = ( x − 1 x) 3. R (y (q)) , where r gives a farmer’s revenue as a function of corn yield per acre, and y gives the corn yield as a function of the quantity, q, of fertilizer. The long arrow represents gf as a single function.
Let's look at another composite function example.
Suppose f is a function, then the composition of function f with itself will be (f∘f)(x) = f(f(x)) let us understand this with an example: Given the function f(x) = 3x + 5 and g (x) = 2x3 2 x 3.find ( gof) (x) and ( fog) (x). Examples and solutions to help gcse maths students learn about composite functions. Examples, solutions, and lessons to help high school students learn how to write a function that describes a relationship between two quantities.
Function f and g are defined by f ( x) = ( x 2 − 2 x) and g ( x) = 3 x + 4.
Learn more about composition of functions here.