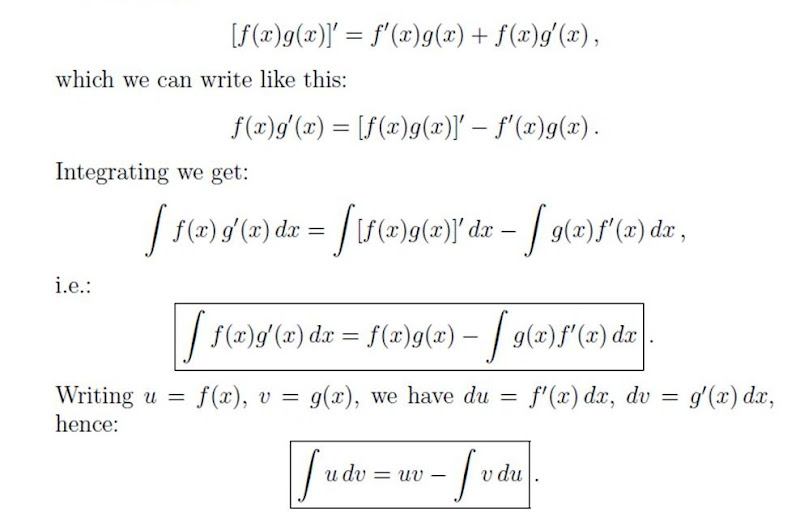In a way, it’s very similar to the product rule, which allowed you to find the derivative for two multiplied functions. → given the following integral, what derivative rule might we try to “reverse” to evaluate the integral 1 x x. For example, you would use integration by parts for ∫x · ln(x) or ∫ xe 5x.
Integration by Parts Proof YouTube
Integration by parts is a special method of integration that is often useful when two functions are multiplied together, but is also helpful in other ways.
The product rule and integration by parts deriving the formula start by writing out the product rule:
Usually, if any function is a power of x or a polynomial in x, then we take it as the first function. To calculate the integration by parts, take f as the first function and g as the second function, then this formula may be pronounced as: You will see plenty of examples soon, but first let us see the rule: Integration by parts rule is not applicable for functions such as \[\int \sqrt{x sin x dx}\].
Integration by reverse chain rule.
You must learn this formula. In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. Thus z x cos( x ) dx = x sin( x ) z sin( x ) dx = x sin( x )+cos( x )+ c: With the product rule, you labeled one function “f”, the other “g”, and then.
V = sin( x ):
(fg)' = f'g + fg'. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more. By the integration by parts formula, z x 2 sin( x ) dx = x 2 cos( x ) z ( cos( x )) 2xdx = x 2 cos( x )+2 z x cos( x ) dx: Same deal with this short form notation for integration by parts.
D/dx [f (x)·g (x)] = f' (x)·g (x) + f (x)·g' (x) becomes.
This is cumbersome, so we usually abbreviate by u = f ( x), v = g ( x) so that d u = f ′ ( x) d x and d v = g ′ ( x) d x. Integration by parts is based on the product rule: Integration by substitution is based on the chain rule. What is integration by parts?
Integration by parts is used to integrate when you have a product (multiplication) of two functions.
( 4 x 2 + 2 x). Dv = cos( x ) dx: This calculus video tutorial provides a basic introduction into integration by parts. Let’s take a close look at the following example of applying the chain rule to differentiate, then reverse its order to obtain the result of its integration.
So in your case we have f ( x) = x 5 and φ ( t) = 2 t + 3:
∫ u d v = u v − ∫ v d u. This one a bit deeper: ∫ a b f ( φ ( t)) φ ′ ( t) d t = ∫ φ ( a) φ ( b) f ( x) d x. To reverse the product rule we also have a method, called integration by parts.
∫ ( 2 t + 3) 5 d t = ∫ 1 2 ( ( 2 t + 3) 5 ⋅ 2) d t = 1 2 ∫ x 5 d x = 1 12 x 6 + c = 1 12 ( 2 t + 3) 6 + c.
( x 3 + x), log e. Now we need to use integration by parts again for the second integral. However, in cases where another function is an inverse trigonometric. Madas question 1 carry out each of the following integrations.
It explains how to use integration by parts to find the indefinite int.
To do this integral we will need to use integration by parts so let’s derive the integration by parts formula. By using this website, you agree to our cookie policy. The chain rule for integration is the integration by substitution. D dx sinx2 = sinx2 × d dx x2 = sinx2 ×2x = 2xsinx2 2xsinx2 = d dx sinx2 ∴ ∫ 2xsinx2dx = sinx2 +c d d x sin.
∫ (f g)′dx =∫ f ′g +f g′dx ∫ ( f g) ′ d x = ∫ f ′ g + f g ′ d x.
The formula is given by: U is the function u(x) v is the function v(x) u' is the derivative of the function u(x) Combine with the rst equation, we get, This article talks about the development of integration by parts:
We do not add any constant while finding the integral of the second function.
Ex2+5x,cos(x3 +x),loge(4x2 +2x) e x 2 + 5 x, cos. Solve for € d dx [u(x)⋅v(x)]= du dx ⋅v(x)+u(x)⋅ dv dx € u(x)⋅ dv dx: Now, integrate both sides of this. Integration by parts → the substitution rule for integrals allowed us to “reverse” the chain rule for derivatives and solve integrals such as 87 2 2 5 x x dx.
∫ f ( x) g ′ ( x) d x = f ( x) g ( x) − ∫ g ( x) f ′ ( x) d x.
( ) ( ) 3 1 12 24 53 10 ∫ u v dx = u ∫ v dx − ∫ u' (∫ v dx) dx. We’ll start with the product rule.





![[10000ダウンロード済み√] ƒ‚ƒ“ƒXƒg i‰» ƒŒƒxƒ‹ 149901G(x)=x+3](https://i.ytimg.com/vi/aMKajIwy7Mo/maxresdefault.jpg)