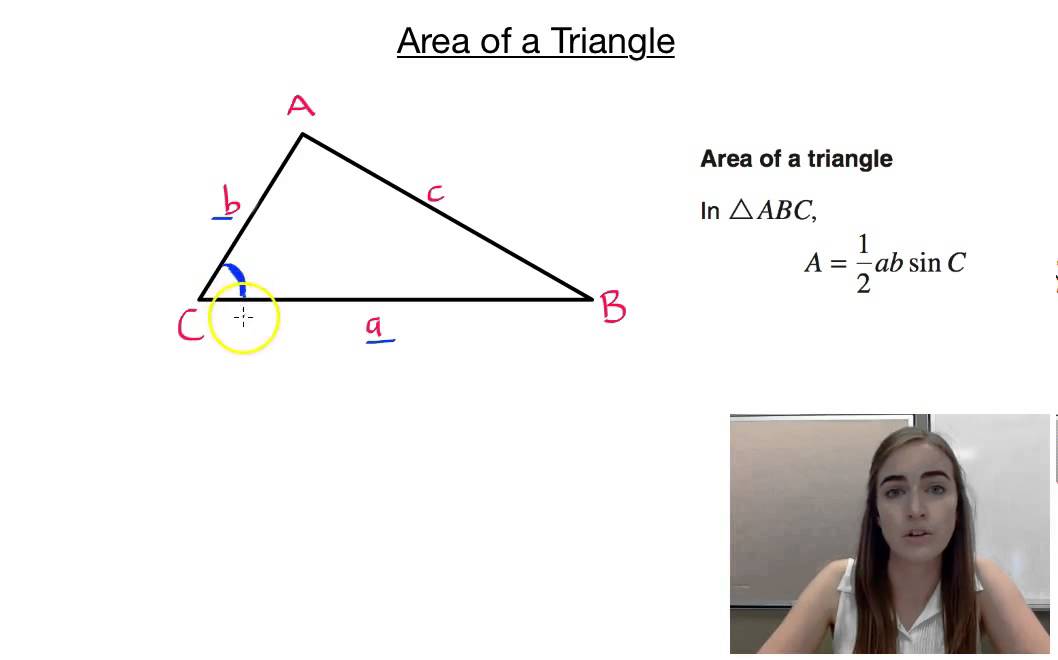
\triangle {a} {b} {m} ab m. Now, if any two sides and the angle between them are given, then the formulas to calculate the area of a triangle is given by: Area = ½ × (c) × (b × sin a) which can be simplified to:
Proofs of sine rule, cosine rule, area of a triangle
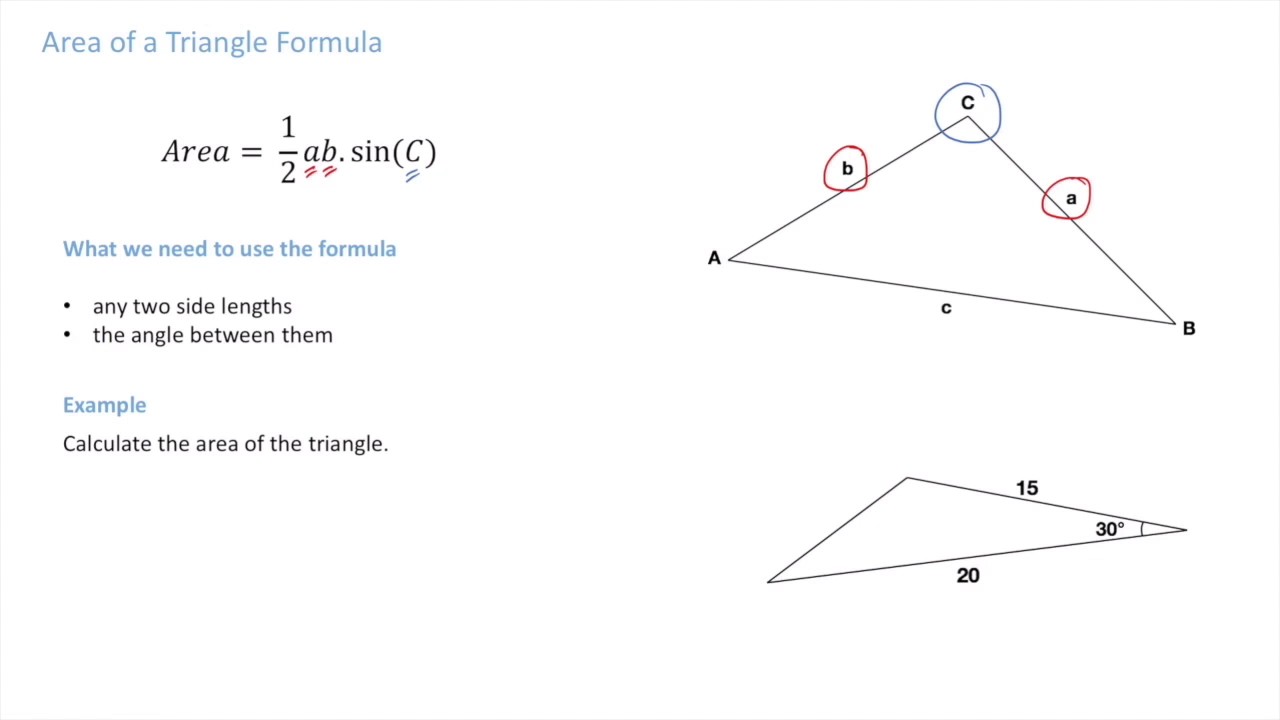
It may be necessary to rearrange the formula.
The most common formula for the area of a triangle would be:
Multiplying both sides of the equation by 10, and solving for the height goes as follows: Cosine rule (the law of cosine): Substituting this new expression for the height, h, into the general formula for the area of a triangle gives: Given, sin a = 0.5 = 5/10 = ½.
Area (∆abc) = ½ ab sin c.
Area = ½ × base × height. = 1 2 × a b × b m × sin ∠ a b m. Area of triangle = ½ ab sinc = 7x (0.965) = 6.755x.
By changing the labels on the triangle we can also get:
Similarly, what are the formulas for triangles? Sina a = sinb b = sinc c. \[\text{area of a triangle} = \frac{1}{2} bc \sin{a}\] \[\text{area} = \frac{1}{2} \times 7.1 \times 5.2 \sin{42}\] area = 12.4 cm 2. =\dfrac { {1}} { {2}}\times {a} {b}\times {b} {m}\times {\sin}\angle {a} {b} {m} =.
Area = ½ × base(b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function.
Use the sine formula to find the side {eq}mn {/eq} and then calculate the area of the triangle. Area = = a² * sin(β) * sin(γ) / (2 * sin(β + γ)) Up to 10% cash back finding the area of a triangle using sine you are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the length of the perpendicular to the base from the opposite vertex. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle.
Area (∆abc) = ½ ca sin b.
Area of triangle = (1/2) ⋅ (ac sin b) = (1/2) ⋅ (x) (14) sin 75. As a consequence of the law of sine, we can neatly put a formula for the area of a triangle: The height is b × sin a. Area = (1 / 2) b c sin(a) = (1 / 2) c a sin(b) = (1 / 2) a b sin(c) how to use the calculator here we assume that we are given sides a and b and the angle between them c.
Where a and b can be any two sides and.
Area = ½ ab sin c. Area = (1 / 2) b c sin(a) = (1 / 2) c a sin(b) = (1 / 2) a b sin(c) how to use the calculator here we assume that we are given sides a and b and the angle between them c. Therefore, we get the general formula Round your answer to the nearest hundredth.
Area = 1 2 bc sin a.
So, the value of x is 22.2 cm. Osea neri | last updated: 4.8 / 5 (20 votes)the area of any triangle can be calculated with a simple trigonometric formula, using the product of the measures of two consecutive sides by. These formulas are very easy to remember and also to calculate.
For example, if, in ∆abc, a = 30° and b = 2, c = 4 in units.
$$\begin {align} \text {height} &= 10 \times \sin (50^ {\circ}) \\ &= 10 \times 0.766 \\ &= 7.66 \end. We know the base is c, and can work out the height: Therefore, h = b sin c. Area of abc = 1 2absinc.
Enter sides a and b and angle c in degrees as positive real.
Improve your math knowledge with free questions in area of a triangle: So, the area of the given triangle is 23.13 cm 2. Sine formula and thousands of other math skills. The area area of a triangle given two of its sides and the angle they make is given by one of these 3 formulas:
This video explains how to determine the area of a triangle using the sine function.
Although the figure is an acute triangle, you can see from the discussion in the previous section that h = b sin c holds when the triangle is right or obtuse as well. Since the area of the triangle is half the base a times the height h, therefore the area also equals half of ab sin c. Areaδ = ½ ab sin c. Find the area of the triangle.
Enter sides a and b and angle c in degrees as positive real numbers and press enter.
Area (∆abc) = ½ bc sin a. Sinθ s i n θ = opposite hypotenuse o p p o s i t e h y p o t e n u s e sinθ s i n θ = 10cm 12cm 10 c m 12 c m sinθ s i n θ = 0.83. Area of triangle = (1/2) ⋅ (bc sin a) = (1/2) ⋅ (7.8) ⋅ (6.4) sin 112 = (1/2) ⋅ (7.8) ⋅ (6.4) (0.927) = 23.13 cm 2. If sin a = 0.5, then find the value of x from the following figure.
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
It allows us to find the area of a triangle when we know the lengths of two sides and the size of angle between them. Given, opposite side = 10 cm hypotenuse = 12 cm.