Arrow_back back to sine rule, cosine rule and area of a triangle sine rule, cosine rule and area of a triangle: 1 yd² 6) a triangle with two sides that measure 6 m and 8 m with an included angle of 137°. (angle opposite to third side).
MEDIAN Don Steward mathematics teaching 0.5 a b sin C
Substitute in the area formula.
Answers included + links to worked examples if students need a little help.
Assume we know the formula for the area of a triangle area = 1 2 (base)(height) 1.(sas) do as many of the following problems as are necessary for you to develop a process that you can describe in question 2. When using this formula, the sides of the triangle are labelled a, b and c and the angle opposite side c is labelled c. Substitute them in the formula a = bh/2 and obtain the. Worksheets (including example and extension).
If sas is given and h is unknown, m a can be written sin a = h/b therefore, multiplying produces.
Using sine to calculate the area of a triangle means that we can find the area knowing only the measures of two sides and an angle of the triangle. Using sine to calculate the area of a triangle. Example, solutions, videos, and lessons to help high school students learn how to derive the formula a = 1/2 ab sin (c) for the area of a triangle by drawing an auxiliary line from a vertex perpendicular to the opposite side. Apply the formula a = 1/2 * base * height;
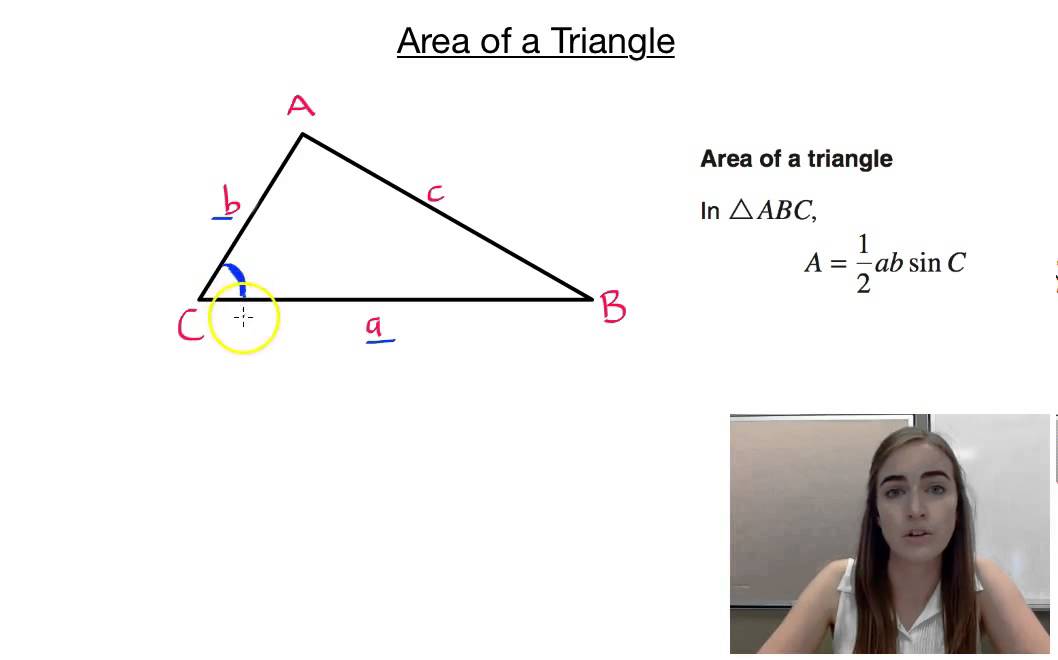
This formula is derived from the area of a triangle formula, a=1/2bh for any triangle abc with side a opposite a, side b opposite b and side c opposite c, height h is represented by a line perpendicular to the base of the triangle.
Where the letters 'a' and 'b' express any two sides of the triangle, and c represents the included angle. Replacing this new value of height in the general formula for calculating the area of a triangle. Using the standard formula for the area of a triangle, we can derive a formula for using sine to calculate the area of a triangle. In calculating the area of a triangle, why do you multiply by 1/2?
The base length (b) and altitude (h) are depicted on the figure.
Area of a triangle worksheet. Area = 1 2 × (yz) × (xz) × sin(z) 39 = 1 2(12)(13)sin(z) solve for z. Xy = √(xz)2 − (yz)2 = √132 − 122 = √169 − 144 = √25 = 5. In each case, nd h.
This handout, which presents right triangles and other triangles as geometric shapes for calculating area, makes great material for 5th grade and 6th grade.
Let not finding the area of geometric shapes trip you up anymore! Normal powerpoint lesson with which you can use a clicker / mouse / keyboard to continue animations and show solutions.; Whether you want a homework, some cover work, or a lovely bit of extra practise, this is the place for you. The students have to then put the cards in order showing how the formula for the area of a triangle using sine has been developed.
Area of triangle = 1/2 × base × height the following formula is used to find the area of non right triangles.
This array of 5th grade printable worksheets on area of triangles comprises problems in three different formats, with integer dimensions offered in two levels. Here is a power point that introduces this topic and includes some examples. Area of triangle = 1/2 ab sin c. Using sine to find the area of a triangle.
Round your answer to the nearest tenth.
So, the area of the given triangle is 53cm 2. And best of all they all (well, most!) come with answers. The height of the triangle can now be written as b sin c. Multiplying the above equation by b, we get:b sin c = h.
This is useful when we don’t know the length of the base or the height of the triangle.
Area of triangle= 1/2 × side 1 × side 2 × sin? 18+ awesome triangle area worksheet pdf from worksheetdaily.blogspot.com 8 in 4 in 7 yd 10 yd 6 ft t. You may see this referred to as the sas formula for the area of a triangle. Up to 10% cash back use the pythagorean theorem to find the length of the third side of the triangle.
The formula area = (1/2)absin(c) can be used to find the area of any triangle.
Area of triangle = (1/2) ⋅ (bc sin a) = (1/2) ⋅ (12.2) ⋅ (10.6) sin 125 = (1/2) ⋅ (12.2) ⋅ (10.6) (0.819) = 52.95 cm 2. The area of a triangle using sine. Areaδ = ½ ab sin c. 𝐴 𝐵 𝐶 is a triangle where 𝐴 𝐵 = 1 8 c m, 𝑚 ∠ 𝐵 = 6 0 ∘ and the area of the triangle is 7 4 √ 3 cm 2.
Enter sides a and b and angle c in degrees as positive real numbers and press enter.
Now, you have lengths of the three sides and the area of the triangle. Derivation and practice of a new area formula for triangles using the sine function. Because a triangle is essentially a split rectangle. Finding area of triangle using the formula half base times height.
With this derived formula, we aren't required to.
Find the area of a parallelogram with sides 6.4 cm and 8.7 cm and one interior angle 64 o. The two attached word documents are two versions of a match up type activity. Area of a triangle using sine. The area area of a triangle given two of its sides and the angle they make is given by one of these 3 formulas:
Area = (1 / 2) b c sin(a) = (1 / 2) c a sin(b) = (1 / 2) a b sin(c) how to use the calculator here we assume that we are given sides a and b and the angle between them c.
1) 6 cm 8 cm 87° 24 cm² 2) 5 in 6 in 140° 9.6 in² 3) 3 yd 8 yd 98° 11.9 yd² 4) 7 in 4 in 96° 13.9 in² 5) a triangle with two sides that measure 6 yd and 2 yd with an included angle of 10°. With this new formula, we no longer have to rely on finding the altitude (height) of a triangle in order to find its area. Find length 𝐵 𝐶 giving the answer to two decimal places. Now, if we know two
Find the area of each figure.
Dependent on ability, this lesson could be split into two full lessons. One full lesson on finding the area of a triangle using 1/2absinc. Up to 24% cash back the area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. These worksheets will teach students how to use the formula for the area triangle to calculate the area of triangles using trigonometry.
A common mistake on this worksheet will be to think that angle b is 90 degrees.
A= 1/2 ab sin c. This formula is derived from the area of a triangle formula, a=1/2bh for any triangle abc with side a opposite a, side b opposite b and side c opposite c, height h is represented by a line perpendicular to the base of the triangle.