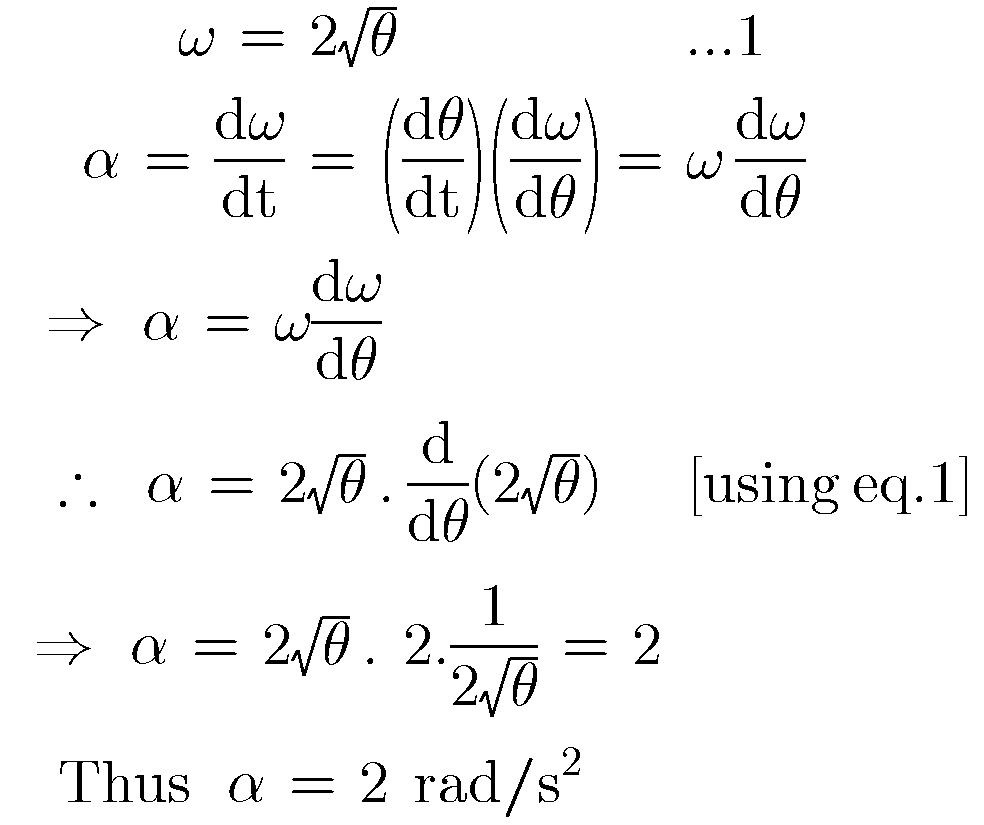By the cosine law it is seen that: Θ f = θ 0 + ω 0 t + 1 2 α t 2. V = ½ (v + v0) [4] substitute the first equation of motion [1] into this equation [4] and simplify with the intent of eliminating v.
How to use Angular Kinematic (Rotational Motion) Equations
Your support will help mit opencourseware continue to offer high quality educational resources for free.
5 rows multiply both the sides by the radius r, \ (r\omega = \frac {r\delta \theta} {\delta t}\) the term \.
Comparison of angular and translational quantities 𝜃 𝜔 𝑣 1. Angular velocity from angular displacement and angular acceleration. And finally, solve for s as a function of t. To make a donation or to view additional materials from hundreds of mit
Equations of motion, torque, angular momentum of rigid bodies the following content is provided under a creative commons license.
Angular displacement from angular velocity and angular acceleration. For example g()(θ))(1,1 = m1.lcm1.g.cos(()θ1))(+ m2.g.[][lcm2.cos(()θ1 +θ2 ))(+. S = u t + 1 2 a t 2. V = ½ [ ( v0 + at ) + v0] v = ½ (2 v0 + at) v = v0 + ½ at [b] now substitute [b] into [a] to eliminate v [vee bar].
This is the velocity an object would follow if.
Differential equation describing the relationship between the moments and angular motion of the two link system. S = s0 + ( v0 + ½ at) t. Just as the terms in translational motion are analogous to the terms in rotational motion, we can write the equations of motion for a particle in rotation. Dω =20×1 = 20 rad/s.
Θ = vit + ½ αt2 angular motion with time cancelled out:
R {\displaystyle r} are constant and. This should come as no. Vandiver goes over finding equations of motion and degrees of freedom, the atwoods machine and rotating mass shaker problems, students' questions about dh/dt and torque, angular momentum for rigid bodies, and the mass moment of inertia matrix, i. Using coriolis’ theorem again for the time derivative of angular velocity, we can evaluate the rotational.
In physics, angular frequency ω (also referred to by the terms angular speed, radial frequency, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate.it refers to the angular displacement per unit time (for example, in rotation) or the rate of change of the phase of a sinusoidal waveform (for example, in oscillations and waves),.
R o = 600 rpm f = 0 rpm = 50 rev. \end{align*} \] note how the form of the equations is identical to the uam equations. In purely rotational (circular) motion, the equations of angular kinematics are: As shown in the diagram, the crank pin, crank center and piston pin form triangle nop.
Ω = δθ / δt angular acceleration:
Α = δω / δt angular displacement: The tangential velocity v v v describes the velocity of an object tangent to its path in rotational motion at angular frequency ω \omega ω and radius r r r. 2 rda n m1i 600 62.8 rad/s min 1 rev 60 s V = u + at s = ut + ½ at2 v2 = u2 + 2as
3 rows this is obtained by breaking the motion up into infinitely many infinitely small chunks, which is.
Plugging these into newton’s formula provides us with our first set of equations of motion. Just consider forces on both bodies. = 𝑟𝜃 velocity 𝑣 acceleration 𝑎 = 𝑡 𝛼 = 𝜔 𝑡 equation of motion 𝑥 = 𝑣𝑡 𝜃 = 𝜔𝑡 momentum 𝑝 = 𝑚𝑣? Stay tuned with byju’s for more such interesting articles.
Angular acceleration and rotational motion.
Θ f = θ 0 + ω 0 t + 1 2 α t 2. On the first using acceleration in polar coordinates we get. − t r ^ = m a → = m ( ( r ¨ − r ω 2) r ^ + ( 2 r ˙ ω + r ω ˙) ϕ ^) so 2 r ˙ ω + r ω ˙ = 0 which when multiplied by r gives d d t ( r 2 ω) = 0, which is precisely your conservation of angular momentum r 2 ω = r 0 2 ω 0. We follow a similar procedure to solve for the angular acceleration and rotational law of motion.
The equations which describe uniformly accelerated angular motion are:
A disk (r = 50 cm), rotating at 600 rev/min comes to a stop after making 50 rev. V = u + a t. 3 rows first kinematic equation of angular motion. The first angular equation of motion is the.
Ω f = ω 0 + α t.
Concepts and quantities linear motion rotational motion position 𝑥 arc length? = 1 2?𝜔 2 relationship between linear and angular speed for a rotating disc of radius (provided that there is no slipping) 𝑣 = 𝑟𝜔 table 1: