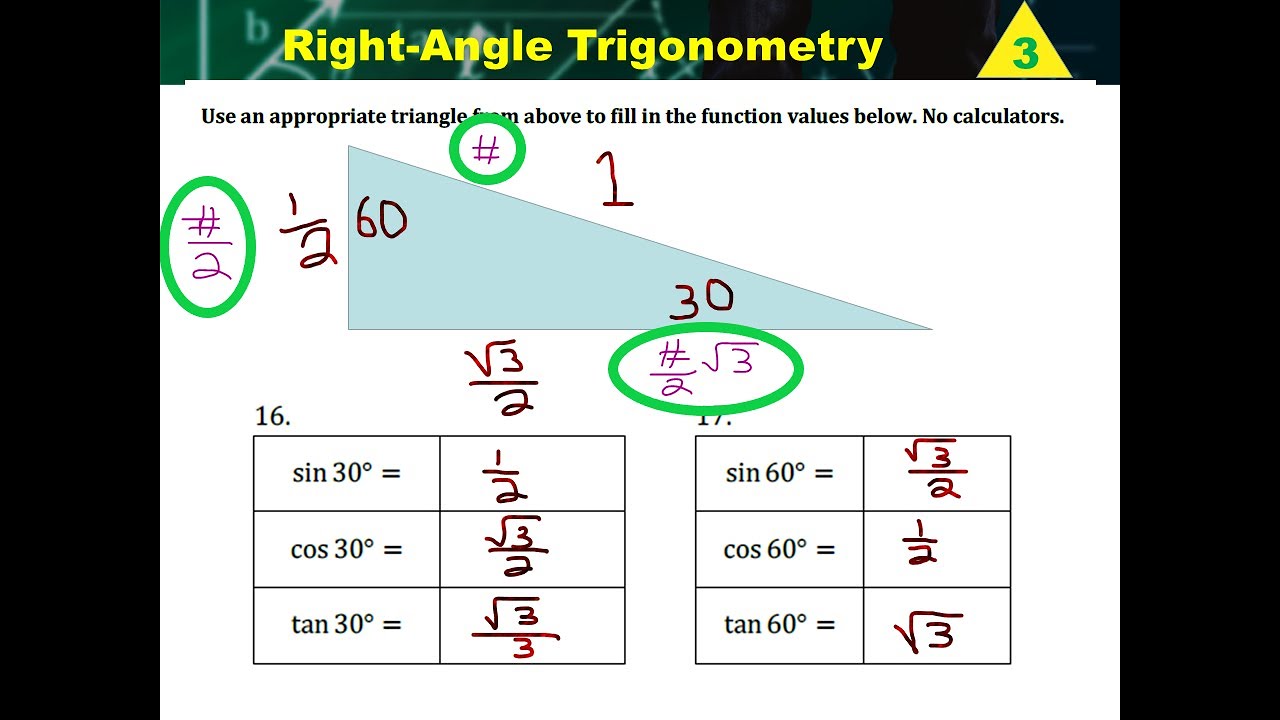
A/c = sin (30°) = 1/2 so c = 2a. 1) u92 2 v 45° 2) x y 42 45° 3) x y 10 45° 4) u v 32 45° 5) x y 22 45° 6) x y 6 2 The sine and cosine of 30° to find out the others sides lengths:
Trigonometry The "Why" Behind Our "Special" Triangles
Ii) what is the length of a throw from the shortstop position to 1 st base if the short stop is midway between 2nd and 3rd base?
60° x = 223, y = 22 12) u293 v 30° u = 58, v = 29 13) a36 b 60° a = 243, b = 123 14) x y 43 30° x = 83, y = 12 15) xy 45 60° x = 90, y = 453 16) x 323 y 30° x = 64, y = 32 17) 40 x y 30° x = 203, y = 20 18) x 333 2 y 30° x = 33, y = 33 2
There are 15 questions hung around the room (lift the flap style). Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another. Find the length of the hypotenuse of a right triangle if the lengths of the other two sides are 4 inches and 4√3 inches. Square both sides ⇒ (x√3) 2 = 36 ⇒ 3x 2 = 36.
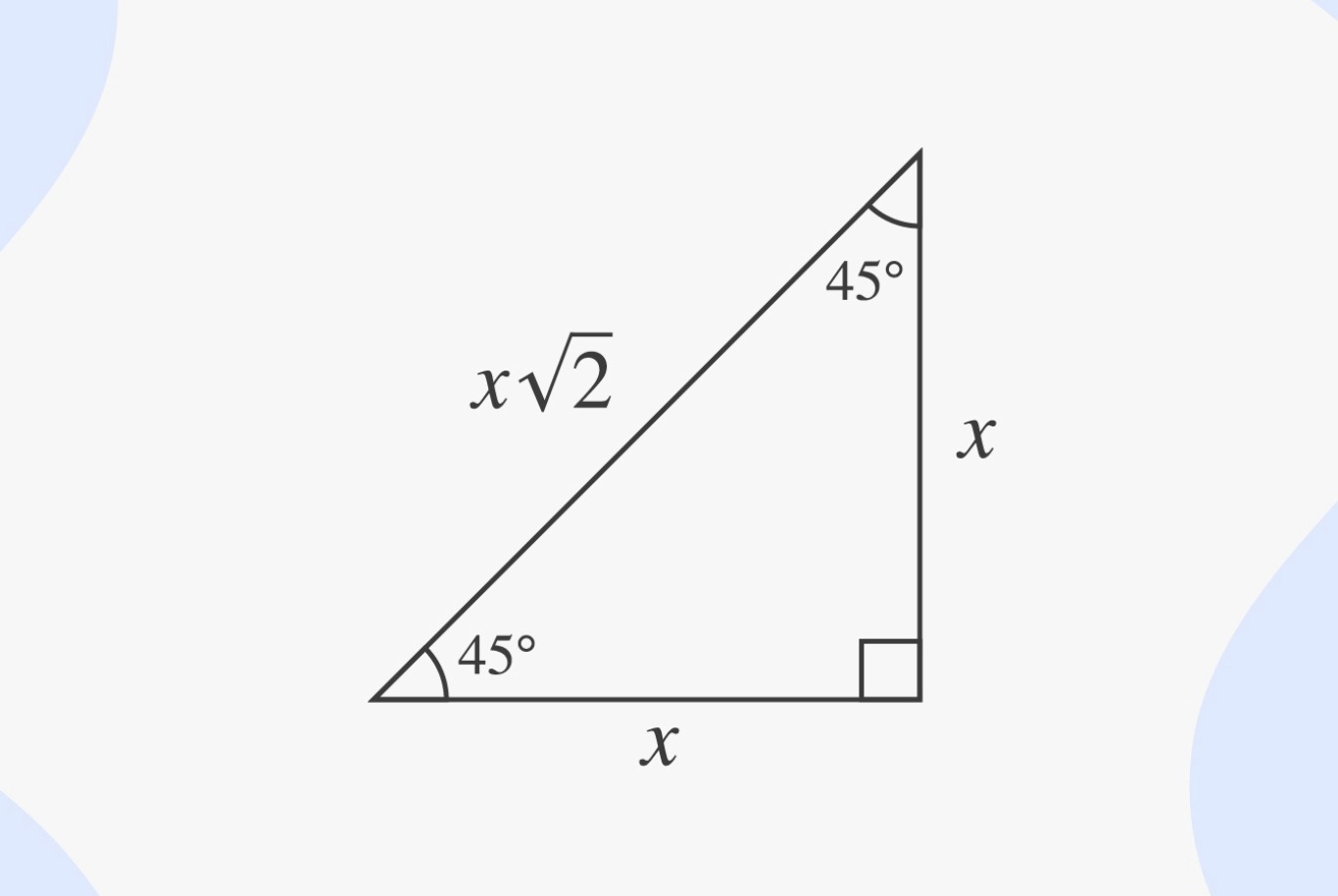
Find the missing side of the 45 45 90 triangle.
If you are familiar with the trigonometric basics, you can use, e.g. ⇒ x√3 = 6 inches. In terms of strategy, another point: So, the side lengths of the triangle are as follows:
If that is the case, then the hypotenuse will always be.
A right triangle has a 45 degree angle, and the hypotenuse has a length of 8 ft. 1) x 20 y 45° 2) a63 b 30° 3) x 72 y 45° 4) x y17 60° Leave your answers as radicals in simplest form. A right triangle has a 60 degree angle, and the leg adjacent to that angle has a length of 7 in.
Find the length of the other leg.
The length of the hypotenuse is 3√2 inches. Notice that the first two answers feature a √3 and a √2 term, and this is clearly a geometry question. Working in pairs, the students answer each question. Leave your answers as radicals in simplest form.
Find the lengths of the other two sides of a right triangle if the length of the hypotenuse is 4√2 inches and one of the angles is 45°.
B/c = sin (60°) = √3/2 so b = c√3/2 = a√3. Up to 24% cash back 1. Test the ratio of the lengths to see if it fits the n:n√3:2n ratio. So, x√3 = 4√3 and 2x = 8.
Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sides.
Hence, the length of the side ac is 8. Also, if you know two sides of the triangle, you can find the third one from the pythagorean theorem. Find the length of a leg. The hypotenuse of a right triangle with a 30 degree angle has a length of 9 cm.