In order to prevent damage to the organ, the radiologist must angle the rays to the tumor. Calculate the length of its base and. Our final answer is 8√3.
Day 1 HW Special Right Triangles 45 45 90, 30 60 90 YouTube
Also, if you know two sides of the triangle, you can find the third one from the pythagorean theorem.
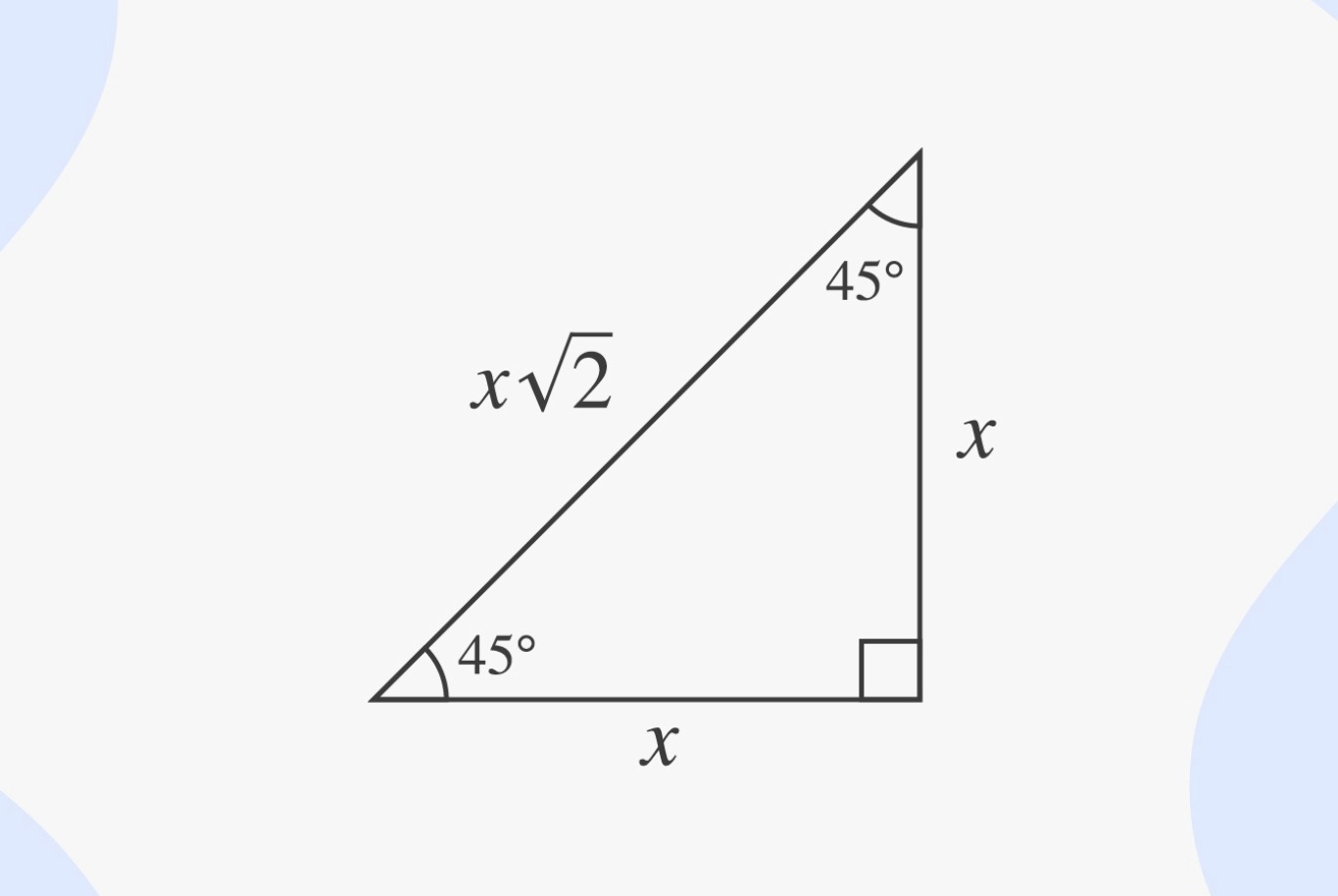
Note that it’s the shape of half a square, cut along the square’s diagonal, and that it’s also an isosceles triangle (both legs have the same length).
So, x√3 = 4√3 and 2x = 8. This is an isosceles right triangle. A/c = √2/2 so c = a√2. 30 60 90 triangle short side, medium side or hypotenuse.
Leave your answers as radicals in simplest form.
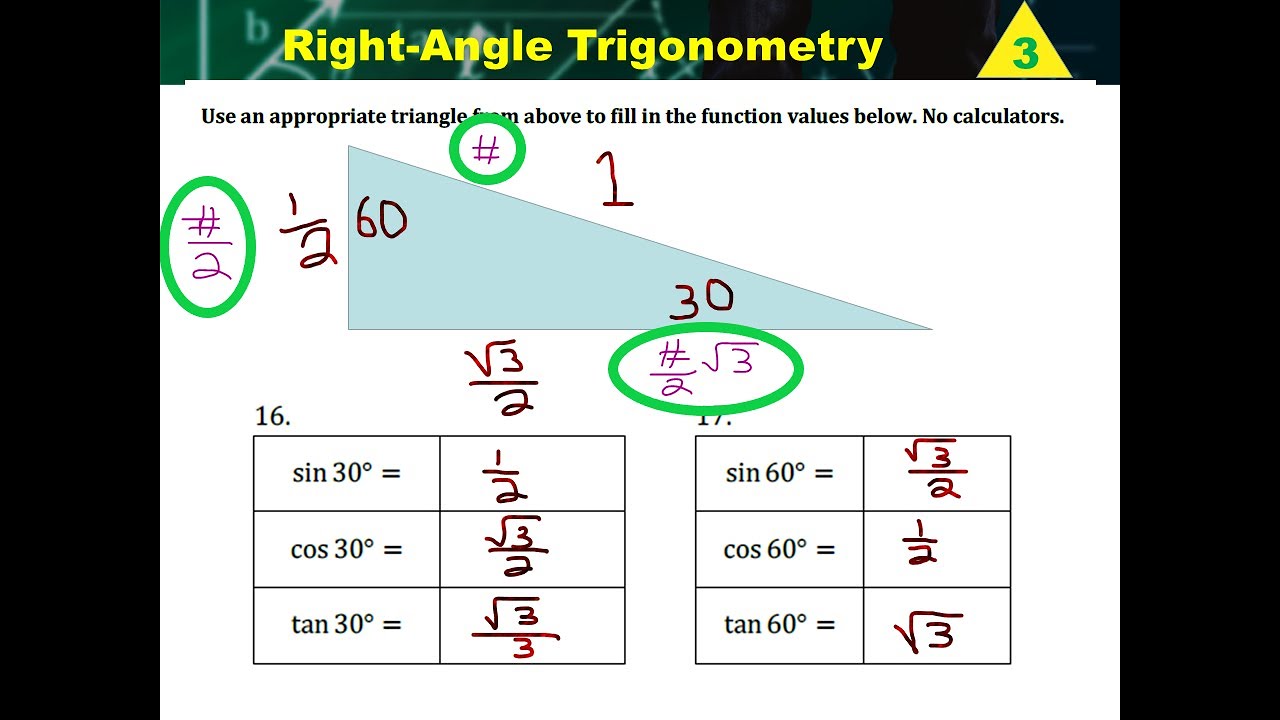
It has angles of 30°, 60°, and 90°. `area = a² / 2`. In our case, one leg is a base and the other is the height, as there is a right angle between them. Long side (opposite the 60 60 degree angle) = x√3 x 3.
A = first side length.
Up to 24% cash back notes: The hypotenuse of the triangle is. So, the side lengths of the triangle are as follows: A patient is being treated with radiotherapy for a tumor that is behind a vital organ.
90° triangle is 6√2 mm.
This page summarizes two types of right triangles which often appear in the study of mathematics and physics. The hypotenuse of a 45°; Relationships between sides of special triangles. Hence, the triangle has the side lengths as follows:
You simply apply pythagorean theorem as follows:
Thanks to all of you who support me on patreon. Here, x√2 = 4√2, so x = 4. Remember, the hypotenuse is always the measure of each. B/c = sin (60°) = √3/2 so b = c√3/2 = a√3.
Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x.
However, the methods described above are more useful as they need to have only one side of the 30 60 90 triangle given. A/c = sin (30°) = 1/2 so c = 2a. Short side (opposite the 30 30 degree angle) = x x. Clicking reset clears all of the boxes.
To find the area of such triangle, use the basic triangle area formula is area = base * height / 2.
As soon as you click that box, the output boxes will automatically get filled in by the calculator. So the area of 45 45 90 triangles is: The 5 choices you have are: 1) x 20 y 45° 2) a63 b 30° 3) x 72 y 45° 4) x y17 60°
B = second side length (equals to first side) c = hypotenuse.