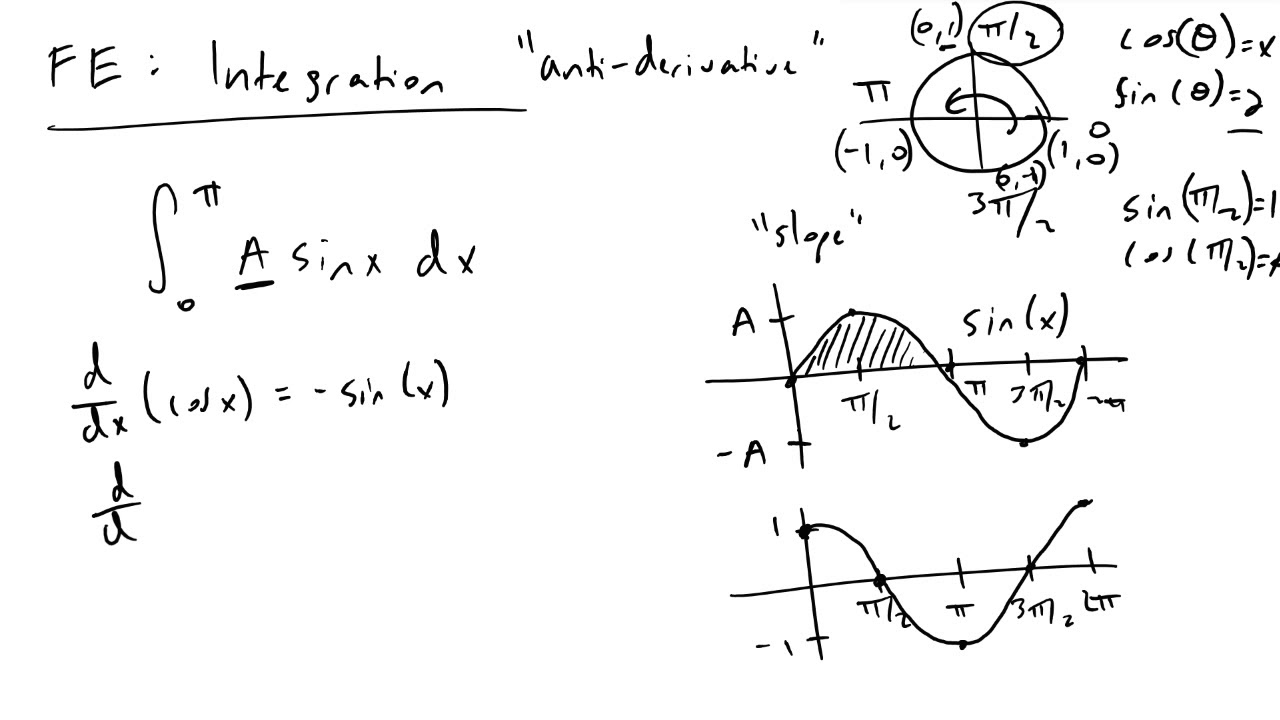
∫(ex) = ex +c ∫ ( e x) = e x + c. Review trigonometric identities 1 trigonometric derivatives we rst need to review the derivative rules for trigonometric functions. Integrating products of powers of sine and cosine;
Integration Formula For Trigonometry Function
Tan1p 2ax+ b 4ac b2.
In class 10th, there are basically three trigonometric identities, which we learn in the trigonometry chapter.
Finding the center of mass. (13) z 1 (x+ a)(x+ b) dx= 1 b a ln a+ x b+ x ; Dx= tan1x (8) z 1 a2+ x2. Cos(ax)cos(bx)dx = 1 2 sin((a b)x) a b + sin((a+b)x) a+b +c.
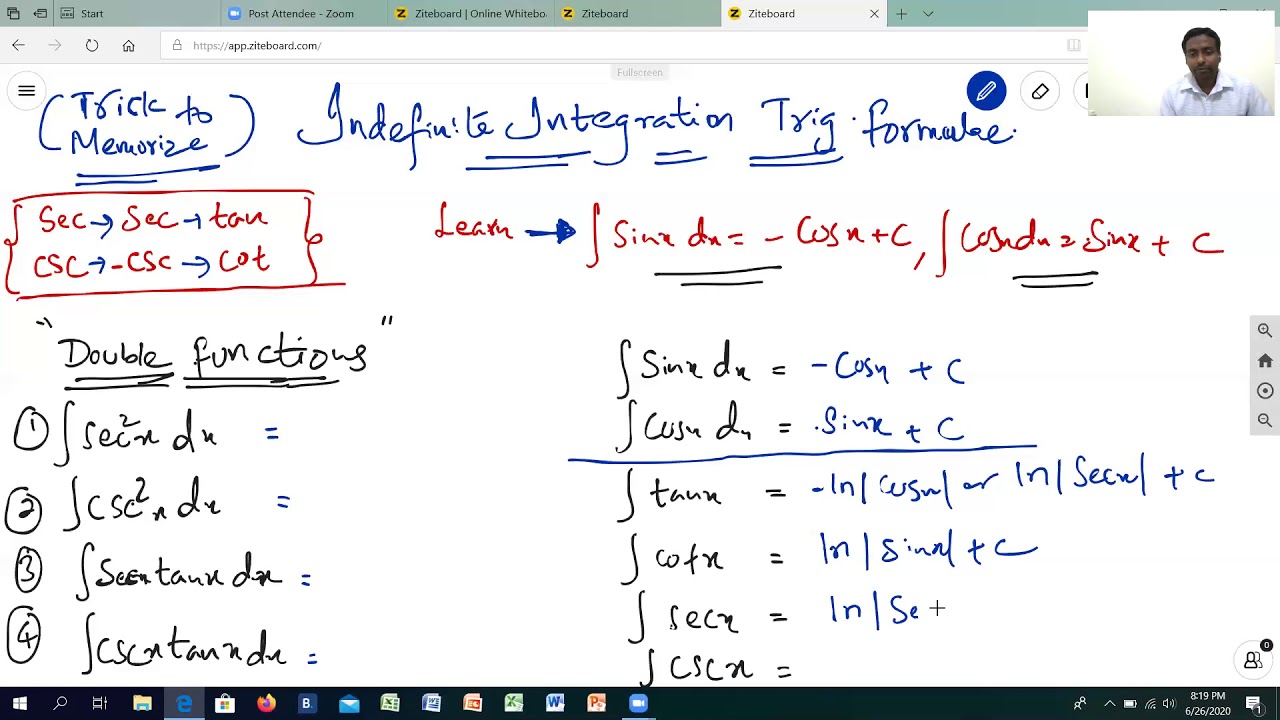
∫sec2 xdx = tanx + c ∫sec x tanxdx = sec x + c
Particularly for trigonometric integrals, the third identity is most helpful if we rearrange and obtain the. X a (11) z x3. Z sin10 xcosx dx 2: Calculus trigonometric derivatives and integrals strategy for evaluating r sinm(x)cosn(x)dx (a) if the power n of cosine is odd (n =2k +1), save one cosine factor and use cos2(x)=1sin2(x)to express the rest of the factors in terms of sine:
∫cot x dx = ln|sin x|.
∫sec x dx = ln|tan x + sec x| + c. Sin 1 y q==y 1 csc y q= Z 1 0 cos(px) cos(qx) x dx= ln q p 6. A6= b (14) z x (x+ a)2.
Those facts can be turnedinto integration formulas directly.
Trigonometric integrals may 20, 2013 goals: ∫ sec a x d x = 1 a ln | sec a x + tan a x | + c = 1 a ln | tan ( a x 2 + π 4 ) | + c = 1 a artanh ( sin a x ) + c {\displaystyle \int \sec {ax}\,dx={\frac {1}{a}}\ln {\left|\sec {ax}+\tan {ax}\right|}+c={\frac {1}{a}}\ln {\left|\tan {\left({\frac {ax}{2}}+{\frac {\pi }{4}}\right)}\right|}+c={\frac {1}{a}}\operatorname {artanh} {\left(\sin {ax}\right)}+c} In integration we basically take the infinitesimal data as the combination. Z ecosx sinx dx 4:
Below are the list of few formulas for the integration of trigonometric functions:
Z 1 0 sin(px) x dx= 8 <: Z cos2 xtanx dx 7: A.) b.) e.) it is assumed that you are familiar with the following rules of differentiation. A2+ x dx= x atan1.
See integral of the secant function.
Trigonometric identities are the equations that include the trigonometric functions such as sine, cosine, tangent, etc., and are true for all values of angle θ. Opposite sin hypotenuse q= hypotenuse csc opposite q= adjacent cos hypotenuse q= hypotenuse sec adjacent q= opposite tan adjacent q= adjacent cot opposite q= unit circle definition for this definition q is any angle. Cos((a b)x) a b +c the other integrals of products of sine and cosine follow similarly. 1 2 sin((a+b)x)+sin((a b)x) dx = 1 2.
∫(logax) = 1 xlna +c ∫ ( l o g a x) = 1 x l n a + c.
Z sin2 xcos2 x dx 9: For a complete list of antiderivative functions, see lists of integrals. Z 1 0 1 cos(px) x2 dx= ˇp 2 5. Trig cheat sheet definition of the trig functions right triangle definition for this definition we assume that 0 2 p <<q or 0°<q<°90.
If a 6= b, then:
The integral ∫cos2 xdx can be handled via formula (10)above. De nite integrals of trig functions note: ∫cos x dx = sin x + c. Generally, if the function is any trigonometric function, and is its derivative, in all formulas the constant a is.
Z ˇ=2 0 sin2 xdx= z ˇ=2 0 cos2 xdx= ˇ 4 2.
For antiderivatives involving both exponential and trigonometric functions, see list of integrals of exponential functions. A2+ x dx= 1 2 x2. There are two which are the most important and come up the most: In a simple straight language integration can be defined as the measure, which basically assigns numbers to the several functions.the numbers are basically assigned which may describe the displacement,volume or area etc of such concerned function.
Start studying trig identities integrals.
Basic mathematics formulas differential and integral || mathematics basic formulas 2022 | important formulas 2022 | differential and integral formulas | pl. Dx= 1 a tan1x a (9) z x a2+ x dx= 1 2 lnja2+ x2j (10) z x2. 1 2 a2lnja2+ x2j (12) z 1 ax2+ bx+ c dx= 2 p 4ac b2. Some of the following trigonometry identities may be needed.
∫tan x dx = ln|sec x| + c.
∫(ax) = ax loga +c ∫ ( a x) = a x l o g a + c. Identities and formulas tangent and cotangent identities tan = sin cos cot = cos sin reciprocal identities sin = 1 csc csc = 1 sin cos = 1 sec sec = 1 cos tan = 1 cot cot = 1 tan pythagorean identities sin2 + cos2 = 1 tan2 + 1 = sec2 1 + cot 2 = csc even and odd formulas sin( ) = sin cos( ) = cos tan( ) = tan csc( ) = csc sec( ) = sec cot( ) = cot Z cosx 1 + sin2 x dx 5: Let’s remind ourselves of the main trig identities that are useful to us.
Review the derivatives for trigonometric functions.
Cos2(x) + sin2(x) = 1,sin(2x) = 2cos(x)sin(x),cos(2x) = cos2(x) − sin2(x). 2 1 sin ( ) 1 cos(2 )x 2 sin tan cos x x x 1 sec cos x x cos( ) cos( ) x x 22sin ( ) cos ( ) 1xx 2 1 cos ( ) 1 cos(2 )x 2 cos cot sin x x x 1 csc sin x x sin( ) sin( ) x x 22tan ( ) 1 sec ( )x x geometry fomulas: Z 1 0 cos(px) cos(qx. In the following formulas all letters are positive.
In the past, we will have a difficult time integrating these three functions.
Sin(ax)sin(bx)dx = 1 2 sin((a b)x) a b. Learn vocabulary, terms, and more with flashcards, games, and other study tools. Integrals of trigonometric functions ∫sin cosxdx x c= − + ∫cos sinxdx x c= + ∫tan ln secxdx x c= + ∫sec ln tan secxdx x x c= + + sin sin cos2 1( ) 2 ∫ xdx x x x c= − + cos sin cos2 1 ( ) 2 ∫ xdx x x x c= + + ∫tan tan2 xdx x x c= − + ∫sec tan2 xdx x c= + integrals of exponential and logarithmic functions ∫ln lnxdx x x x c= − + ( ) 1 1 2 ln ln 1 1 n n x xdx x cn x x n n Trigonometric identities for class 10.
Do integrals involving trigonometric functions.
Integrals involving sine and cosine; ˇ=2 p>0 0 p= 0 ˇ=2 p1 0</strong> sin2 px x2 = ˇp 2 4. ∫(c) = x+c ∫ ( c) = x + c ( where c is a constant) ∫(cx) = cx2 2 +c ∫ ( c x) = c x 2 2 + c ( where c is a constant) ∫(xn) = xn+1 n+1 ∫ ( x n) = x n + 1 n + 1. Z sin2 x dx 8:
∫(1 x) = ln|x|+c ∫ ( 1 x) = l n | x | + c.
A s2 1 area of a triangle: Z sin3 xcos2 x dx 3: